意味不明すぎる“6つの係数”について分かりやすく解説
社会人の学び直しに特化した【Schoo(スクー)】がおすすめ!
金融リテラシーを高めて、もっと豊かで楽しい人生を送るヒントを見つけよう!
7000本の授業が見放題!社会人向けオンライン学習動画【Schoo(スクー)】

出やがったな、“6つの係数“

おっ、かし先生が珍しく険しい表情。

いやね、実は大学生の頃に始めてFPについて学習したんだけど、 “6つの係数“ が意味不明すぎて挫折した過去があるんだ。

『ライフプランニングと資金計画』から学んでいくと、最初にぶち当た壁が “6つの係数“ って人結構多いよね。

ははは、先生にも苦手分野があるんだね♪私なら余裕だけど!

じゃあきりちゃんこの “現価係数” の表をみても同じこと言える?
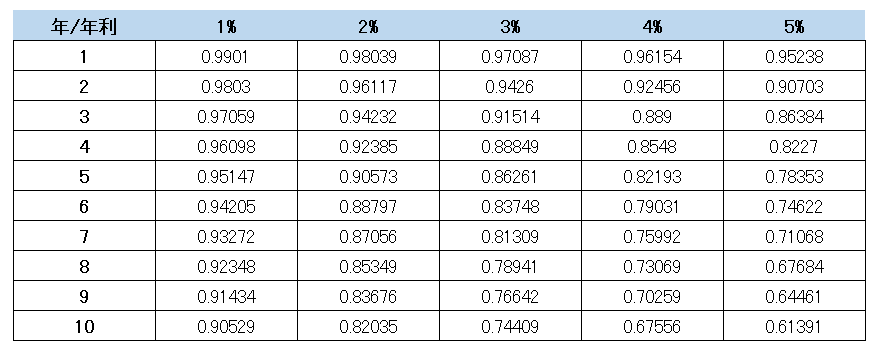

…….。

おやすみぃ💤💤

ほらね!!
目次
苦手意識を持たれる “6つの係数” の理由
「6つの係数」と聞くと、それだけでアレルギー反応を起こす人も多いかもしれません。
FP試験でも頻出のテーマではありますが、「意味がわからない」「覚えられない」と苦手意識を持つ受験者が少なくないのも事実です。
まず一つ目の壁は、名前のカタさ。
終価係数、年金現価係数、資本回収係数、減債基金係数、、、と、どれも見慣れない言葉ばかりで、まるで呪文のよう。
最初から「難しそう」と感じてしまい、思考が止まってしまう原因になります。
次に、数字や計算が絡むことへの苦手意識です。
「将来の100万円の価値は?」「今から毎年いくら積み立てると将来いくらになる?」といった内容は、数学が苦手な人にとってハードルが高く感じられがち。
数字がズラリと並んだ係数表を見ると、それだけで思わず目をそらしたくなります、、、。
でも実は、それぞれの係数が「何を表しているのか」さえちゃんと理解できれば、計算そのものはとってもシンプルなんです。
「なんでそんな計算するの?」「この数字って何の意味?」っていう疑問が残ったままだと、
すべてが暗号みたいに見えてしまいます。
でも逆に、「あっ、これはローンの返済額を出すための係数なんだ!」とか「これは将来のために毎年いくら積み立てればいいかを出すんだ!」って、意味がつかめると、スッと理解できるようになります。
“6つの係数” を正しく理解するためには、 “複利” の知識が必須

“6つの係数” を正しく理解するためには大前提として “複利” の知識が必須なんだよね。

“複利” ?…ああ!そういえば前に解説してくれてたやつね!

複利のことよく分からない!っていう方は先に こちら の記事を見に行ってね。
“6つの係数” は全部に “複利” が関係してくるから、正しく理解するためには必須知識だよ!
6つの係数表がややこしく見えてしまう理由は、
「複利」という仕組みが関係しています。
単利は、元本に対して毎年同じ額が増えるため、計算も数字もシンプルです。
でも複利は、元本だけでなく「増えた分」にも利回りがかかるため、
年数が増えるごとに数字の伸び方がどんどん変化していきます。
その結果、6つの係数表では
「同じ年数でも利率によって数字の差が大きくなったり、金額がキレイに揃わなかったり」して、
一見するとややこしく感じられてしまうんです。
6つの係数①:現価係数
将来のお金が、現在の価値でいくらになるかを計算するための係数です。
“現”在の“価”値を知りたいので現価係数!
たとえば、、、
「年利5%で複利運用して、5年後100万円に増やしたい!そのためには今のお金っていくら必要?」
というように、未来のお金を“現在の金額”に置き換えるときに使います。
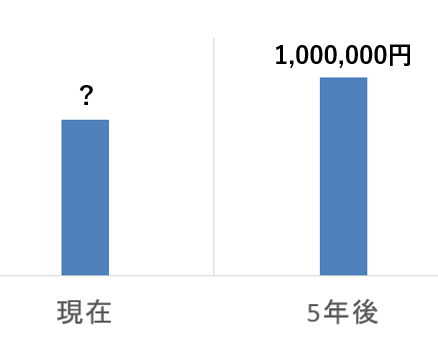

単利ならまだしも、複利で求めるとなると計算式は…
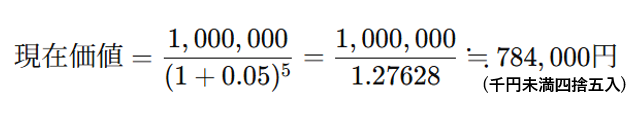

ああそっか!複利って計算超めんどくさいから、係数表を使って一発で答えを導き出してくれるってこと?

う、うん!その通りだよきりちゃん!!(びっくりした…いつもなら意味不明な計算式みたら発狂してたのに。)
じゃあ5%の複利運用で5年後ということは…
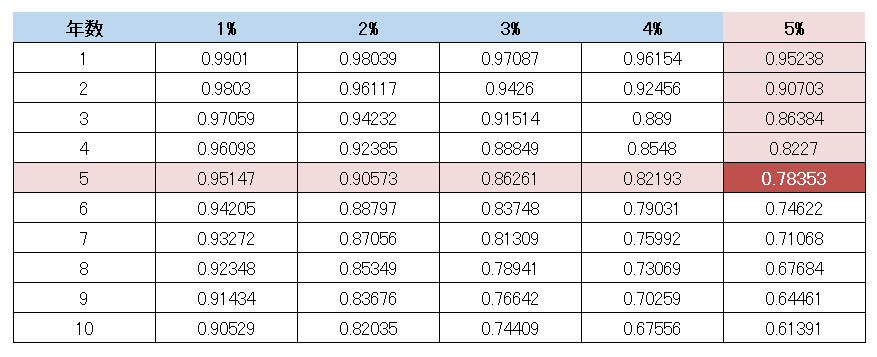

『0.78353!』ここに将来のお金100万円を×して万円未満四捨五入したら『784,000円』やったー!超簡単♪

そう!正解!さすがだよきりちゃん!!
複利の計算って超面倒なんだけど、この表を使って金額を掛けたらあっという間に答えが出せるんだ!
(うわー、正直あと3,000字は解説必要かなと覚悟してたのに。)

さっきから心の声聞こえてますけど💢
複利の仕組みを理解していても、
毎回電卓で計算をするのは面倒ですよね。
でも、係数表を使えば、複利計算がサクッと終わる非常に便利なツールになります。
時間をかけずにスマートに資金計画を立てたい人には、まさに強い味方になるんです。
6つの係数②:終価係数
「今あるお金が、複利運用すると将来いくらになるか」を計算するための係数です。
“終”わりの“価”値を知りたいので終価係数!
たとえば、、、
「手持ちの100万円を年利3%で複利運用してら、10年後はいくらになってる?」
というように、今の手持ちのお金を“将来の金額”に置き換えるときに使います。
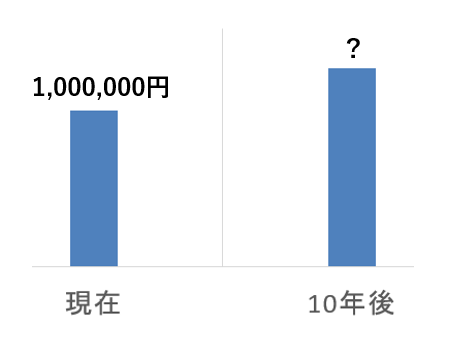

察してる人も多いかもしれないけど、“現価係数” の逆ってだけだね。
終価係数と現価係数は、お金の時間的な価値を“進めるか戻すか”の違いだけです。
- 終価係数:今あるお金が将来いくらになるか(未来へ進める)
- 現価係数:将来のお金が今いくらの価値か(現在へ戻す)
つまり、終価係数は “未来に向かう計算”、現価係数は “現在に戻す計算” それだけです。
それでは、終価係数の表で実際に計算してみましょう。
年利3%、10年間の複利運用なので…
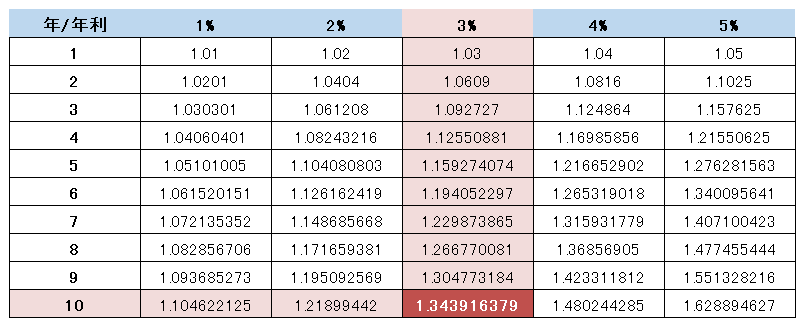
答えは『 100万円 × 1.343916379 = 1,344万円(万円未満四捨五入) 』となります。
複利運用することで、100万円だった価値が10年後には1,344万円にまで増加したことが分かりますね。
6つの係数③:年金終価係数
年金終価係数は、毎年一定額を積み立てていったときに、将来いくらになるかを求めるための係数です。
つまり、「積立投資の合計が将来いくらになるか」を計算するときに使う便利な数字です。
ここでの「年金」は、「老後にもらう年金」ではなくて、
一定額を毎年積み立てるお金という意味です。
「毎“年”積み立てたお“金”の最“終”的な“価”値で覚えましょう。」
終価係数との違いは、終価係数は「1回だけの投資」に対して、年金終価係数は「毎年コツコツ積み立てる投資」に使う係数となります。
では、実際に計算してみましょう。
「毎年100万円を積立投資して、年利5%で複利運用したら、5年後はいくらになってる?」
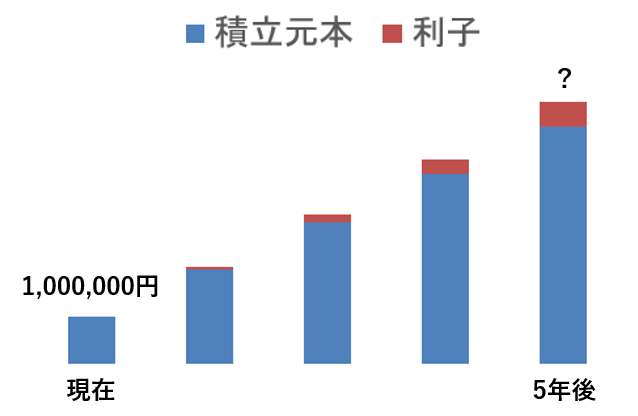

ちょっとずつだけど、複利の力で利子が年々増加していってるのが分かるね。
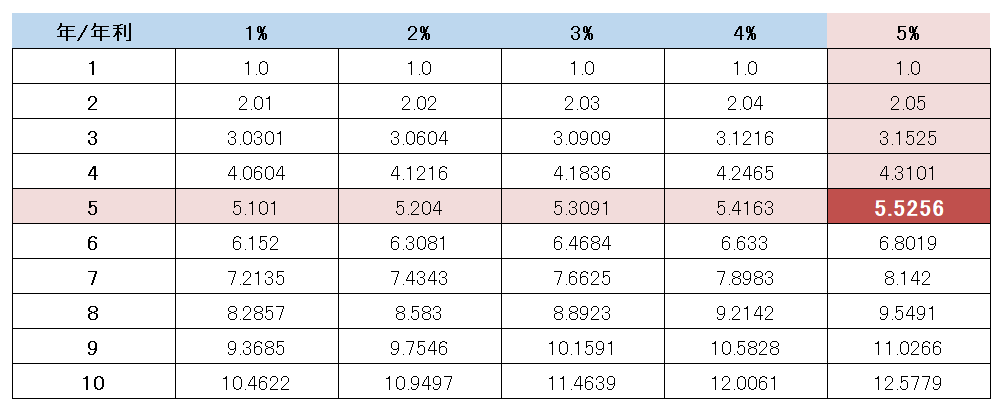
答えは『 100万円 × 5.5256 = 553万円(万円未満四捨五入) 』となります。
ただ家に保管していただけだと500万円ですが、複利運用をすることで、553万円にまで増加しましたね。
6つの係数④:減債基金係数

へ?なにこの漢字どういう意味?💦

元々は企業や国が借金(“債”券)を返済(“減”らす)していくために、毎年少しずつお金を貯める(“基金”)目的で使われていた係数だからこんな呼び方なんだけど、まあそんな考え込まないで💦
将来のある時点で一定の金額を用意するために、毎年いくらずつ積み立てればよいかを計算するための係数です。
たとえば、
「5年後に100万円を用意したい!年利5%の複利運用で毎年積み立てるとしたら、毎年いくらずつ積み立てればいい?」
といった計算時に使用します。
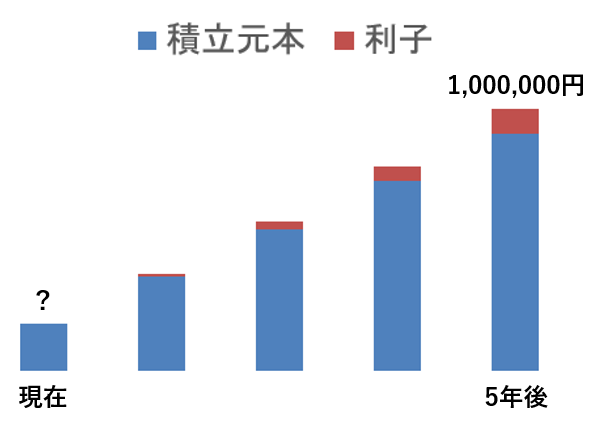

こちらも察しの通り、先ほど紹介した”年金終価係数” の逆ってだけだね。
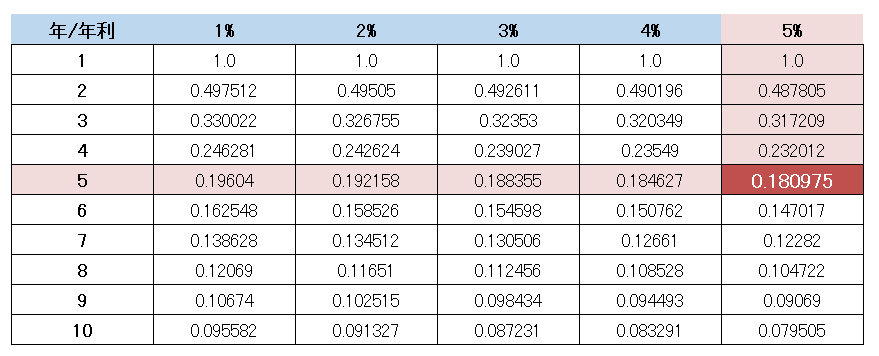
答えは『 100万円 × 0.180975 = 18万円(万円未満四捨五入) 』となります。
毎年18万円積み立てることで、目標金額の100万円に到達できると計算できますね。
6つの係数⑤:年金現価係数
毎年一定額を受け取れるお金(“年金”など)を、“現”在の“価”値でいくらか?
を計算するための係数です。
たとえば、
「年利4%で複利運用しながら毎年70万円ずつ5年間受け取りたい!その場合今いくら必要?」
といった計算時に使用できます。
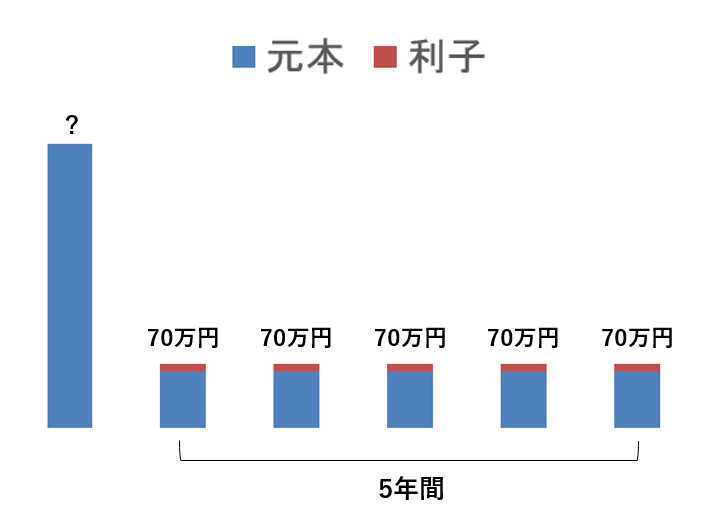

受け取りたい金額である70万円を、該当する数値に当てはめちゃえば、他の係数と同様に簡単に答えが出せちゃうよ。
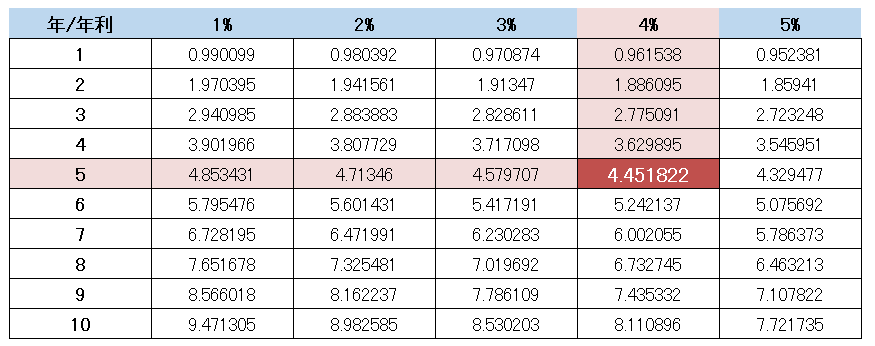
答えは『 70万円 × 4.451822 = 312万円(万円未満四捨五入) 』となります。
普通なら『70万円×5年間』で350万円は必要だと思うところ、複利運用することで、312万円の用意があれば、毎年70万円を受け取ることができますね。
6つの係数⑥:資本回収係数

資本回収…?

たとえば「投資した元手(=“資本”)を5年かけて、毎年同じ金額で均等に“回収”していきたい!」というときに、
その「毎年いくらずつ取り崩せばいいか」を計算するのに使える係数だよ。
老後の生活では、「公的年金とは別に、毎年もう少しプラスで〇〇万円くらい欲しいな…」と感じることもあるでしょう。
そんなとき、現役時代に貯めたお金(元手)を、毎年一定額ずつ取り崩して『公的年金+私的年金』でゆとりある老後生活を送る方法があります。
ただし、手元にあるお金をただ取り崩すだけではもったいないので、
どうせならそのお金を複利運用しながら、効率よく取り崩していていくことで、毎年使える金額を増やすことができるのです。
「5,000万円のお金(元手)を年利3%で複利運用しながら20年かけて取り崩す場合、毎年いくらずつ受け取れる?」
こちらの問題を解いてみましょう。
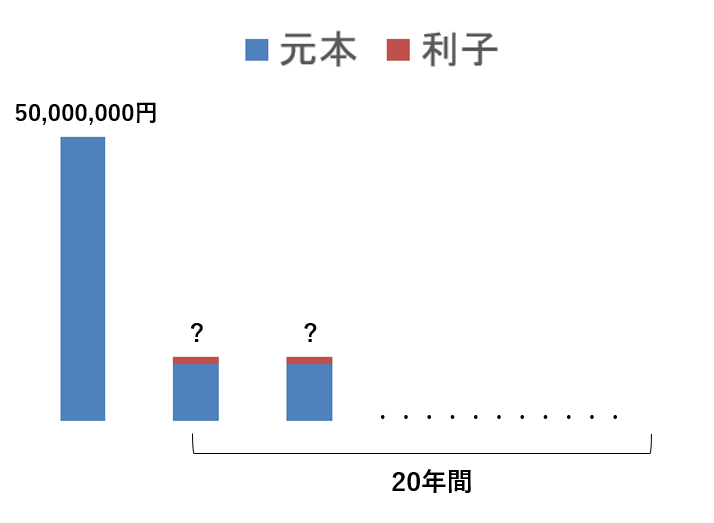

こちらは年金現価係数の逆ってだけだね。
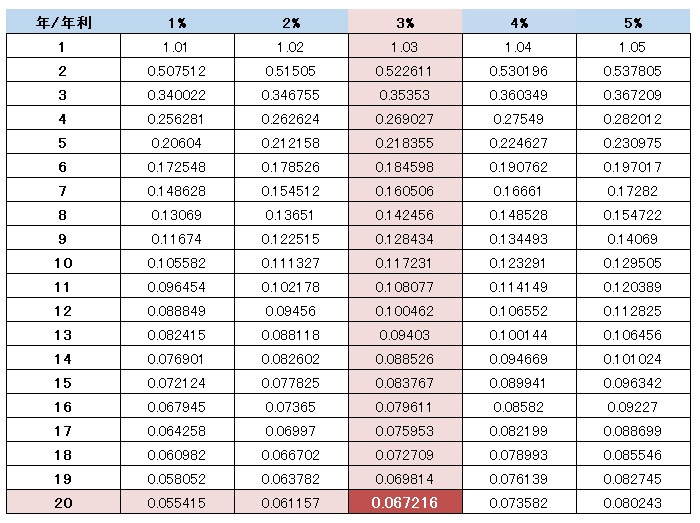
答えは『 5,000万円 × 0.067216 = 336万円(万円未満四捨五入) 』となります。
現時点で5,000万円の元手が準備できれば、20年間は毎年336万円が受け取れると計算できますね。
6つの係数はこの3ペア!
「6つの係数」と聞くと、「えっ、そんなに覚えなきゃいけないの?意味わかんないし、ちょっと嫌だな…」と思ってしまうかもしれません。
でも実は、これまで紹介してきた通り、この6つの係数は3組のペアになっていて、それぞれが対の関係にあるだけなんです。
対の意味と使い方さえ理解できれば、それほど難しいものではありません。
①【現価係数 ↔ 終価係数】
これは、投資資金を最初に「ぽん」と出して複利運用した場合に、
今の金額が将来いくらになるか?またはその逆で、将来必要な金額を今いくら用意すればいいか?
――という現在と未来のお金を行き来する関係です。
②【年金終価係数 ↔ 減債基金係数】
これは、毎年コツコツ積み立てながら複利運用した場合に、
最終的にいくら貯まるか?またはその目標額のために毎年いくら積み立てればいいか?
――という積立額と将来の金額を結ぶ関係です。
③【年金現価係数 ↔ 資本回収係数】
これは、すでに貯まっているお金を複利運用しながら毎年一定額ずつ取り崩すときに、
元手がわかっている場合、「毎年いくら使えるか?」またはその逆に「この毎年の生活費のためには元手がいくら必要か?」
――という一定の取り崩し額とその元手を行き来する関係です。
まとめ:暗記よりお金の流れをイメージしよう!

6つも係数があるって聞いたときは、正直“もうムリ!”って思ったけど、、、
難しい複利計算を一発で解けるすごく便利なツールなんだってわかって、ちょっと感動しちゃった!

うんうん、後はそれぞれがペアになっていて、“どっちを知ってて、どっちを求めたいか”ってだけなんだよね。
現価と終価、積立と目標額、元手と取り崩し額、、、全部対になってるって分かると、すごく整理しやすくなるよ。

いいねその調子!先生なんて、昔は意味も分からず全部丸暗記で突破しちゃってたからね💦
大切なのは係数の意味を理解して『お金の流れをしっかりイメージすること』、本質を理解して実生活でも応用してみよう!
最後に:FPかしの独り言
今回は、「6つの係数」について解説しました!
私自身、大学生の頃に「FP資格は就活に有利らしいよ」という噂を聞いて、よくわからないままFP3級にチャレンジしたのがきっかけでした。
「さあ、やるぞ!」と意気込んでテキストを開いたものの、最初に出てきたのが――6つの係数。
「えっ、なにこれ…意味わかんない!もしかして他の5分野もこんな感じ!?」と絶望し、
勉強開始30分でFP試験の受験を諦めたというのは、今となっては笑い話です。(笑)
でも、今あらためて言えるのは、
この6つの係数は、資金計画を考えるうえで欠かせないツールだということ。
たとえば――
- 減債基金係数を使えば、「将来の夢や目標のために毎年いくら積み立てればいいか?」がわかる。
- 資本回収係数を使えば、「老後資金3,000万円を30年にわたって取り崩すなら、毎年いくら受け取れるか?」を計算できる。
こうした係数は、キャッシュフロー表やライフイベント表をつくるときに非常に役立ちます。
今の貯蓄額をバランスシートで把握し、将来の夢に向かってお金を複利で増やしながら計画的に使っていくためには欠かせない存在です。
とはいえ、個人的にはこの6つの係数、最低でも15年以上の中長期的な計画でないと本来の力を発揮しにくいと感じています。
というのも、現実はそんなにきれいに計算通りにはいかないから。
たとえば、5年後に運用していた株価が大暴落していたら、
複利で増えているどころか、元本割れしているということも普通にあり得ます。
投資の世界は「上がったり下がったり」を繰り返しながら、『数十年というスパンで見れば平均して年5%くらい成長してたね〜』という感覚がちょうどいいんです。
だからこそ、短期的なライフイベントに向けた資金計画を立てるときは要注意。
係数の数値をうのみにせず、
- まずは生活防衛資金として無リスク資産(銀行預金など)をしっかり確保すること。
- その上で、余裕のあるお金を株式などで複利運用していくこと。
このバランス感覚がとにかく大切です。
6つの係数は、うまく使えば心強い道具。
けれど、それを使いこなす前提には「現実的な視点」や「長期的な視野」も欠かせないということを、ぜひ覚えておいてくださいね。
社会人の学び直しに特化した【Schoo(スクー)】がおすすめ!
金融リテラシーを高めて、もっと豊かで楽しい人生を送るヒントを見つけよう!
7000本の授業が見放題!社会人向けオンライン学習動画【Schoo(スクー)】


